피보나치 수열

피보나치 수열이란

0과 1로 시작하여 a -> b -> c -> d - > e -> f 일때 d는 a + b 인값 e는 d + e인 값을 나타내는 수열

즉 0 -> 1 -> 1 -> 2 -> 3 -> 5 -> 8 이런식으로 다음 숫자가 앞의 두 숫자의 합으로 나타내는 수열을 뜻한다

 

재귀 함수를 사용하여 피보나치 수열을 구현할수 있다

#include <iostream>
#include <stdio.h>

using namespace std;
int fibonachi(int n)
{
	if (n <= 1)
		return n;
	else
		return fibonachi(n - 1) + fibonachi((n - 2));
}
int main()
{
	int n = 5;
	int result = fibonachi(n);
	printf("피보나치(%d)의 결과 : %d\n", n, result);
	return 0;
}

 

 

이런식으로 구현한다면 시간복잡도면에서 매우 비효율적이다

왜냐하면 f(4)를 구할려면 f(3)과 f(2)의 값이 필요하고 f(5)를 구할려면 f(4)와 f(3)이 필요하기떄문에

했던 연산을 또하고 또해서 매우 비효율적이다

그래서 f(n)을 미리 구해서 그걸 기억했다가 꺼내서 쓴다면 중복연산을 피하고 효율적일것이다

그걸 Memoization이라고 한다

#include <iostream>
#include <stdio.h>
#include <vector>

using namespace std;
vector<int> mmn;
int fibonachi(int n)
{
	if (n <= 1)
		return n;

	//이미 계산된 값이면 그대로 반환
	if (mmn[n] != -1)
		return mmn[n];

	//계산하고 저장
	mmn[n] = fibonachi(n - 1) + fibonachi(n - 2);
	return mmn[n];
}

 

프로그래머스 의 피보나치 수 라는 문제를 확인해보자

 

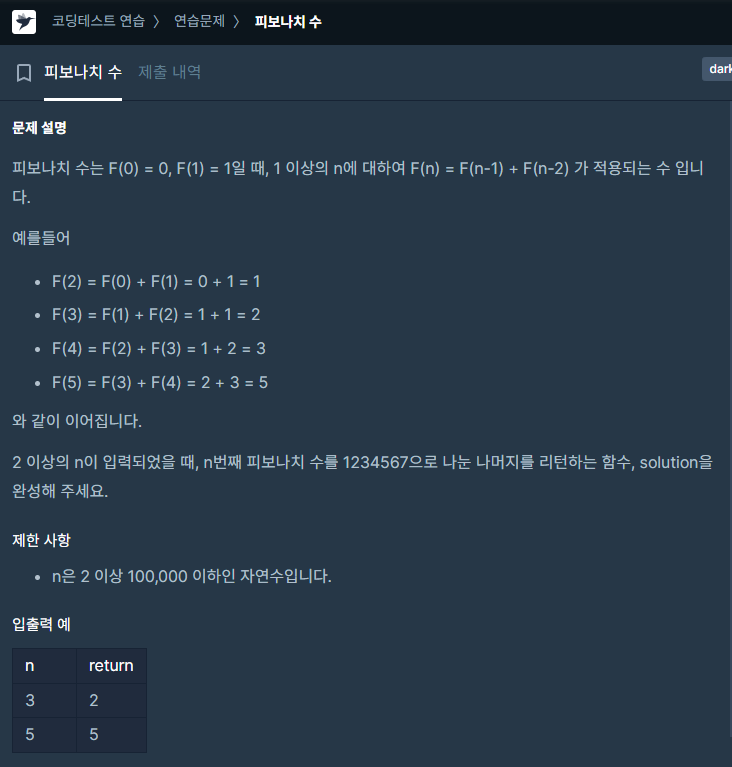
아까 사용한 memoization 방식을 사용하고 조건을 추가해주면된다

#include <string>
#include <vector>

using namespace std;
vector<int> memoization;
int solution(int n) 
{
    const int modNum = 1234567;

    if (memoization.size() <= n)
        memoization = vector<int>(n + 1, -1);

    if (n <= 1)
        return n;

    if (memoization[n] != -1)
        return memoization[n];

    
    memoization[n] = (solution(n - 1) + solution(n - 2)) % modNum;
    return memoization[n];
}