Algorithm - Graph

그래프는 정점과 간선으로 이루어져있다

정점 (Vertex) 는 노드라고 불리며 그래프를 형성하는 기본 단위이다

간선 (Edge)는 정점을 잇는 선을 의미한다. 관계 가 간선의 경우이다

 

방향 그래프

노드 A와 B를 잇는 간선이 한방향으로만 갈수 있을때 방향 그래프라고함

 

양방향 그래프

 

노드 A와 B를 잇는 간선이 양 방향으로 갈수 있을때 양방향 그래프라고 함

 

가중 그래프

간선에 가중치가 부여되며 이러한 그래프를 가중 그래프라고 한다

 

 

그래프의 순회

그래프의 순회에는 크게 DFS, BFS 가 있다

 

그래프의 최단 경로 알고리즘

크게 벨만-포드, 다익스트라, 플로이드-워셜 이 있다

 

사이클이 없는 방향 그래프 (DAG)

그래프에서 정점 A와 B중에 누가 먼저냐고 대한 답을 할수없다 배열인 경우에는 인덱스가 낮은값이 먼저라고 할수있는 선형 구조지만 그래프는 정점간의 순서를 정의할수없는 비선형 구조이기때문이다 하지만 그래프도 어떠한 특수한 경우에 정점간의 순서를 매길수 있고 이러한 그래프를 DAG(Directed Acyclic Graph)라고 한다 이러한 DAG에서 정점의 순서에 따라 정렬하는걸 위상 정렬 이라고 한다

 

최소 신장 트리 (MST)

간선의 가중치가 있는 경우에 간선들의 가중치의 합을 구할 수 있다. 두 정점 간의 경로가 존재하는 선에서 간선을 제거하는 연산을 할수있을때 연산들의 결과로 간선들의 가중치의 합을 가장 작게 만든 그래프를 MST라고 한다

 

 

그래프는 크게

인접 리스트, 인접 행렬, 간선 리스트

3가지가 있다.

인접리스트 (Adjacency List)
노드의 갯수만큼 공간을 확보한 뒤 각 노드를 기준으로 연결된 노드를 저장하는 방식

최단 경로 알고리즘의 다익스트라 알고리즘에 사용

 

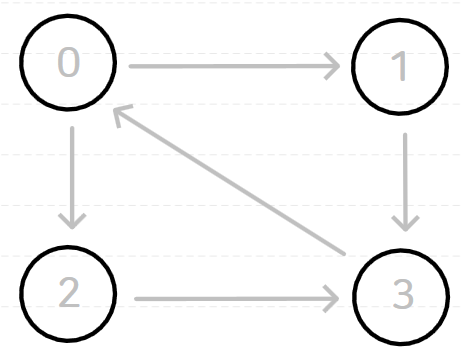
이러한 그래프가 있다

 

해당 그래프를 인접 리스트로 표현하면 2차원 배열이 만들어진다

 

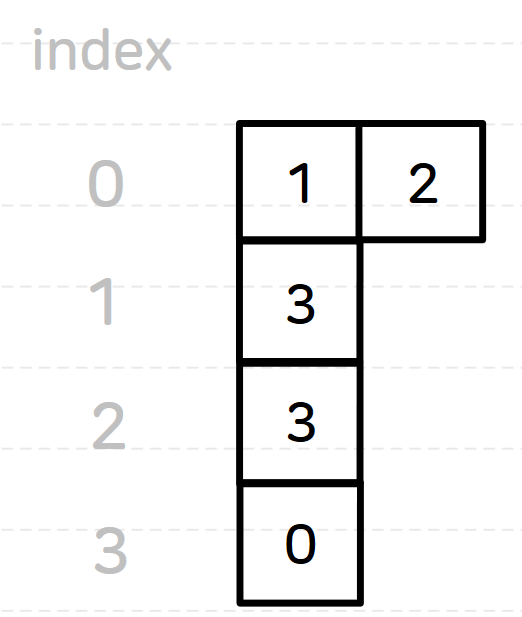
#include <vector>
#include <iostream>

using namespace std;

int main()
{
	vector<vector<int>>adj_list(4);
	adj_list[0].push_back(1);
	adj_list[0].push_back(2);

	adj_list[1].push_back(3);

	adj_list[2].push_back(3);

	adj_list[3].push_back(0);

	for (int i = 0; i < 4; i++)
	{
		for (auto& u : adj_list[i])
		{
			cout << u << ' ';
		}
		cout << '\n';
	}
	return 0;
}

인접 행렬 (Adjacency Materix)
노드의 개수 X 노드의 개수 만큼의 행렬(공간)을 만든 후에 간선을 표현하는 방식

최단 경로 알고리즘의 플로이드- 워셜 알고리즘에 사용

 

다음과 같은 그래프가 있다

 

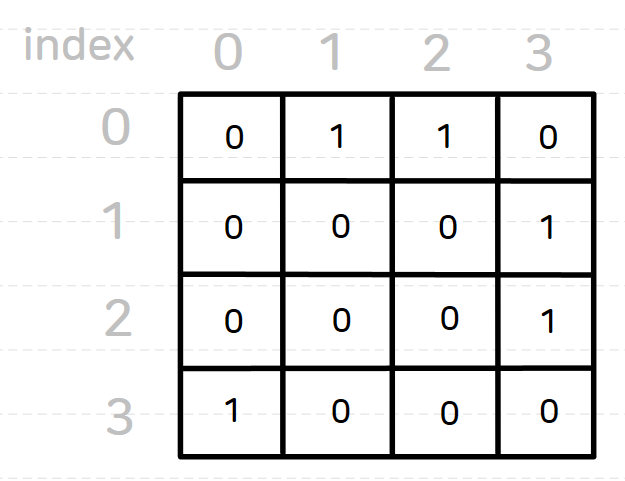
인접 행렬로 표현하면 다음과 같이 노드의 갯수 X 노드의 갯수 크기로 2차원 배열이 만들어진다

해당 adj_materix[A][B]가 1일경우 노드 A에서 노드 B로 가는 간선이 있다는 의미

 

#include <vector>
#include <iostream>

using namespace std;

int main()
{
	vector<vector<int>>adj_matrix(4, vector<int>(4, 0));
	
	adj_matrix[0][1] = 1;
	adj_matrix[0][2] = 1;

	adj_matrix[1][3] = 1;

	adj_matrix[2][3] = 1;

	adj_matrix[3][0] = 1;
	for (int i = 0; i < 4; i++)
	{
		for (auto& u : adj_matrix[i])
		{
			cout << u << ' ';
		}
		cout << '\n';
	}
	return 0;


}

 

간선 리스트(Edge List)
간선의 정보만들 저장하는 방식으로 간선의 갯수 크기의 배열이 만들어진다

최단 경로 알고리즘의 벨만-포드 알고리즘에서 사용

 

또한 이러한 그래프가 주어진다

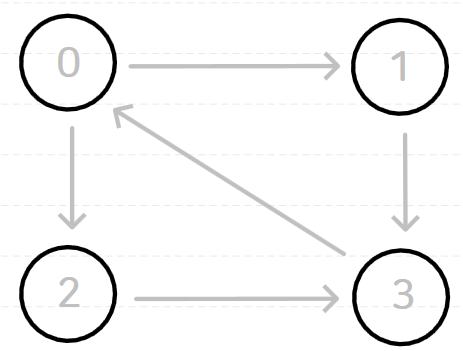
해당 그래프를 간선 리스트로 표현하면 다음사진과 같이

간선의 갯수 크기의 1차원 배열이 만들어진다

 

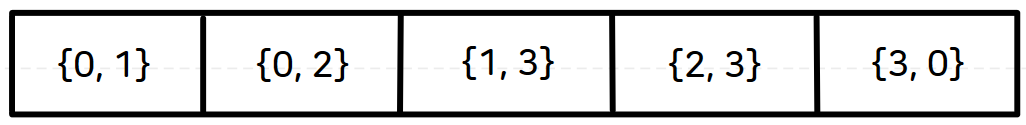
#include <vector>
#include <iostream>

using namespace std;

int main()
{
	vector<array<int,2>> edge_list;

    edge_list.push_back({0, 1});
	edge_list.push_back({ 0, 2 });
	
	edge_list.push_back({ 1, 3 });

	edge_list.push_back({ 2, 3 });
	edge_list.push_back({ 3, 0 });
	for (auto [s, e] : edge_list)
	{
		cout << s << ' ' << e << '\n';
	}
	return 0;



}