정렬(Sorting)이란?
데이터를 어떤 기준에 따라 순서대로 재배치하는 알고리즘을 뜻한다
정렬의 종류에는
버블 정렬(Bubble Sorting)
선택 정렬(Selection Sorting)
삽입 정렬(Insertion Sorting)
퀵 정렬(Quick Sorting)
병합 정렬(Merge Sorting)
등이 있다
버블 정렬(Bubble Sorting)


개념 : 배열의 인접한 두개의 아이템을 선택하고 비교해서
왼쪽의 아이템이 오른쪽 보다 클경우
즉 arr[0] > arr[1] 일경우
배열의 들어있는 원소를 서로 Swap하여 바꾼다
이걸 끝까지 반복하여 배열 전체가 정렬되는것이 버블 정렬 이다
시간복잡도 : O(N^2)
N - 1번의 반복이 필요하기때문에 좋은 알고리즘은 아님
버블정렬의 예시
#include <iostream>
#include <vector>
using namespace std;
void solution(vector<int>&arr)
{
for (int i = 0; i < arr.size(); i++)
{
for (int j = 0; j < arr.size() - 1; j++)
{
//배열의 왼쪽값보다 오른쪽값이 크다면스왑
if (arr[j] > arr[j + 1])
{
//붙어있는 인덱스아이템 서로 스왑
swap(arr[j], arr[j + 1]);
}
}
}
}
int main()
{
vector<int> arr = { 1, 3, 5, 2, 9 };
solution(arr);
for (int x : arr)
{
cout << x << " ";
}
}
선택 정렬(Selection Sorting)
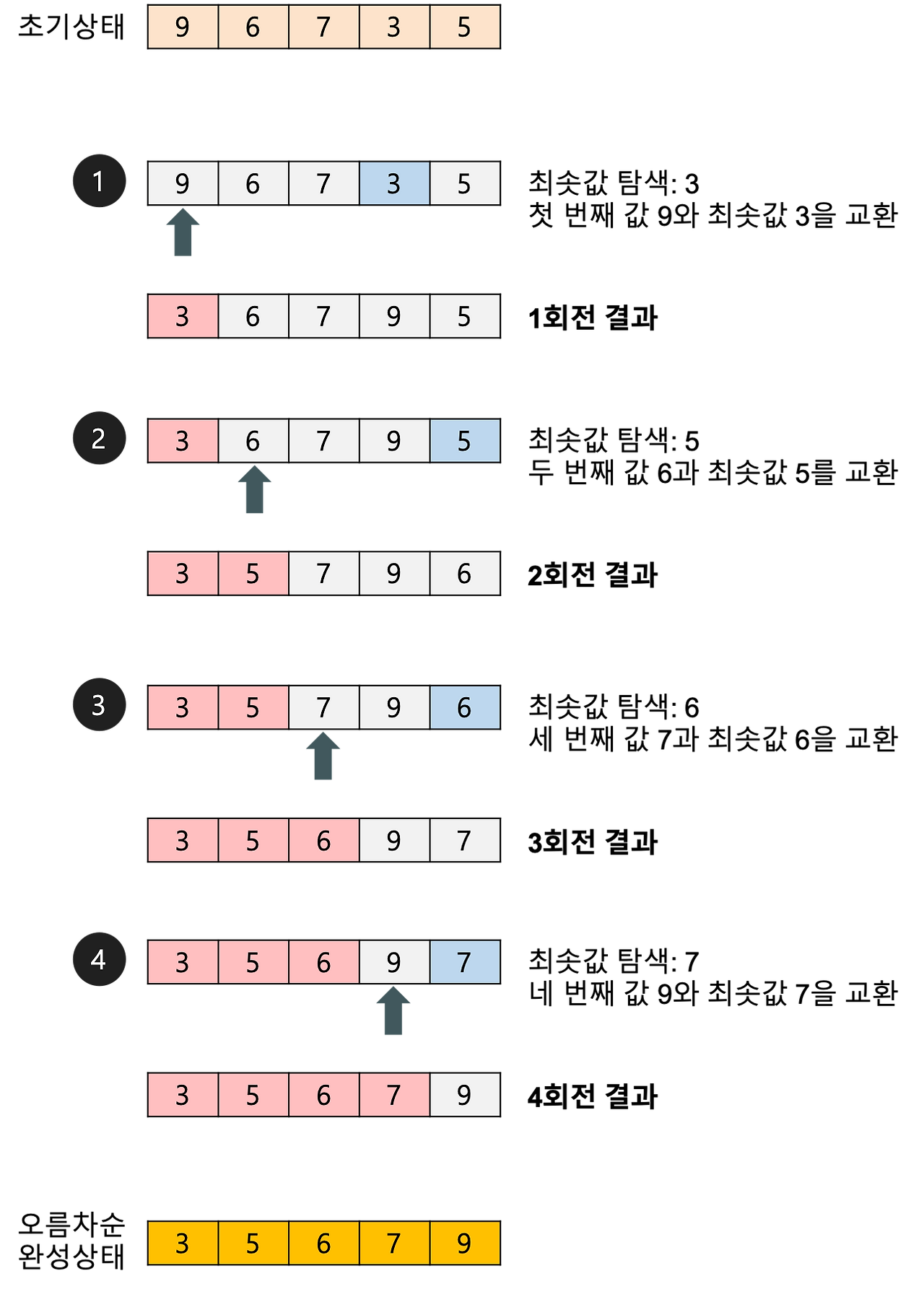
개념 : 배열에서 가장 작은(혹은 가장 큰) 원소를 찾아서 배열의 앞쪽부터 차례대로 자리를 바꾸며 정렬
처음부터 끝가지 탐색해서 최솟값 혹은최대값을 찾고 그 값을 현재 위치의 값과 Swap
배열 끝까지 반복하면 선택정렬이 완성
선택 정렬의 시간복잡도 : O(N^2)
특징 : N번의 스왑을 하지는 않아 버블보다는 좋을수있고 구현이 쉽고 직관적이나
데이터가 많으면 너무 느려서 이것도 그렇게 효율적인 정렬은 아니다
선택 정렬의 예시
#include <iostream>
#include <vector>
using namespace std;
void solution(vector<int>& arr)
{
for (int i = 0; i < arr.size(); i++)
{
//최솟값 초기화
int minIndex = i;
for (int j = i + 1; j < arr.size(); j++)
{
//현재 검사중인 원소가 지금까지 발견한최솟값 보다 작으면
//더 작은값이 발견되었으니 최솟값 위치를 j로 업데이트 한다
if (arr[j] < arr[minIndex])
{
minIndex = j;
}
}
//최솟값이 현재 위치와 다르면 swap
if (minIndex != i)
{
swap(arr[i], arr[minIndex]);
}
}
}
int main()
{
vector<int> arr = { 1, 3, 7, 2, 9 };
solution(arr);
for (int x : arr)
{
cout << x << " ";
}
}
삽입 정렬(Insertion Sorting)


개념 : 배열을 왼쪽부터 차례대로 검사하면서
현재 위치에 값을 왼쪽에 정렬된 부분에 알맞은 위치에 "삽입" 정렬방식
현재 원소를 왼쪽의 정렬된 부분과 비교해가며 적절한 자리로 밀어 넣는 방식
두번쨰 원소부터 시작을 하여 그 원소를 왼쪽의 정렬된 부분과 비교하며
정렬된 부분에서 더 큰원소들을 오른쪽으로 밀어내며 현재 원소를 올바른 위치에 삽입
삽입 정렬의 시간복잡도 : O(N^2)
최선의 경우 O(N)
거의 정렬된 배열에 매우 빠르고 안정 정렬이다
하지만 무작위 데이터에서는 느리다
삽입 정렬의 예시
#include <iostream>
#include <vector>
using namespace std;
void solution(vector<int>& arr)
{
//배열의 두번쨰 원소부터 검사
for (int i = 1; i < arr.size(); i++)
{
//삽입할 원소
int key = arr[i];
//key원소보다 더 왼쪽에 있는 인덱스
int j = i - 1;
//key보다 큰 원소들을 오른쪽으로 한칸 미루기
while (j >= 0 && arr[j] > key)
{
//arr[j]는 현재 비교중인 왼쪽원소
//arr[j + 1]은 그 원소의 오른쪽칸
arr[j + 1] = arr[j];
//원소를 오른쪽으로 밀기
j--;
}
arr[j + 1] = key;
}
}
퀵 정렬(Quick Sorting)

퀵정렬 개념 : 분할 정복 개념 을 사용하는 아주 빠른 정렬알고리즘
작동박식 :
1. Pivot 기준점 하나를 선택한다 ( 배열의 첫번쨰 원소, 마지막원소, 중간값, 랜덤값 여러가지 선택 가능)
2. Pivot 기준으로 분할한다 ( Pivot보다 작은 값은 왼쪽, 큰값은 오른쪽) 작은값 << - Pivot - >> 큰값
3. 왼쪽과 오른쪽 각각을 재귀 호출로 다시 퀵 정렬
4. 분할이 불가능할때 정렬 완료
즉 분할 , 정복, 결합을 실행하면된다
- 분할(Divide): 입력 배열에서 하나의 피벗(Pivot)을 선택하고, 피벗을 기준으로 왼쪽에는 피벗보다 작은 요소들, 오른쪽에는 피벗보다 큰 요소들로 나누어 2개의 부분 배열로 분할한다.
- 정복(Conquer): 각 부분 배열이 충분히 작아질 때까지 같은 방법(분할 정복)을 재귀적으로 적용하여 정렬한다.
- 결합(Combine): 정렬된 왼쪽 배열, 피벗, 정렬된 오른쪽 배열을 순서대로 합쳐 하나의 완전한 정렬 배열을 만든다.
ex) 배열 [ 5, 3, 2, 8, 7, 10, 11 ] 이 있을때 퀵 정렬방식을 사용하면
1. 첫번쨰 원소는 '5' / Pivot = '5'
왼쪽은 pivot보다 작은 [ 3, 2 ]
오른쪽은 pivot보다 큰 [ 8, 7, 10, 11 ]
2. 왼쪽부분 [ 3 , 2 ]
왼쪽부분의 첫 번쨰 원소는 '3' / Pivot = '3'
왼쪽 [ 2 ] -> 원소1개(정렬완료)
오른쪽 = x
3. 오른쪽부분 [ 8. 7. 10, 11]
오른쪽부분의 첫 번째 원소는 '8' / pivot = '8'
왼쪽은 pivot보다 작은 [ 7 ] -> 원소1개(정렬완료)
오른쪽은 pivot보다 큰 [ 10, 11]
4. 오른쪽의 오른쪽부분 [ 10, 11 ]
첫번째 원소 '10' / pivot = '10'
왼쪽 = 없음
오른쪽 = [ 11 ] -> 원소1개(정렬완료)
더이상 분할할수 없을때
최종 정렬 = 왼쪽 + Pivot + 오른쪽
왼쪽 부분 합치는법
[ 3 , 2 ] 정렬 결과
[ 2 ] + 3 + [ ] = [ 2, 3 ]
왼쪽부분 정렬 결과 = [ 2, 3 ]
오른쪽 부분 합치는법[8, 7, 10, 11 ] 정렬 결과[ 7 ] + 8 + [ 10 , 11 ] = [ 7, 8, 10, 11 ]오른쪽부분 정렬 결과 = [ 7, 8, 10, 11 ]
배열 [ 5, 3, 2, 8, 7, 10, 11 ]의 pivot은 첫번째 원소인 '5'
[2, 3] + 5 + [7, 8, 10, 11]
[2, 3, 5, 7, 8, 10, 11] 이 결과값으로 도출된다
장점 : 속도가 매우 빠름
다른 정렬 알고리즘(삽입, 선택, 버블 정렬 등)은 평균적으로 O(N²)의 시간복잡도를 가지지만,
퀵 정렬은 평균적으로 O(N log N)의 시간복잡도를 가진다.
단점 : 정렬된 리스트에 대해서는 퀵정렬이 수행시간이 오히려 더 많이 걸림
퀵 정렬 예시
#include <iostream>
#include <vector>
using namespace std;
void solution(vector<int>& arr)
{
//내부 재귀 함수 정의하기
auto quickSorting = [&](auto&& self, int left, int right) -> void
{
if (left >= right)
{
return;
}
//원소의 가장 첫번째 원소
int pivot = arr[left];
//피봇 기준으로 왼쪽과 오른쪽 탐색할 포인터 초기화
int pivotLeft = left + 1;
int pivotRight = right;
//더이상 교환할 원소가 없을떄까지 반복
while (pivotLeft <= pivotRight)
{
while (pivotLeft <= pivotRight && arr[pivotLeft] <= pivot)
{
pivotLeft++;
}
while (pivotRight >= pivotLeft && arr[pivotRight] >= pivot)
{
pivotRight--;
}
if (pivotLeft > pivotRight)
{
swap(arr[left], arr[pivotRight]);
}
else
{
swap(arr[pivotLeft], arr[pivotRight]);
}
}
//왼쪽 재귀 호출
self(self, left, pivotRight - 1);
//오른쪽 재귀 호출
self(self, pivotRight + 1, right);
};
//초기 호출
quickSorting(quickSorting, 0, arr.size() - 1);
}
int main()
{
vector<int> arr = { 5, 3, 2, 8, 7, 10, 11 };
solution(arr);
for (int x : arr)
{
cout << x << " ";
}
return 0;
}
병합 정렬(Merge Sorting)
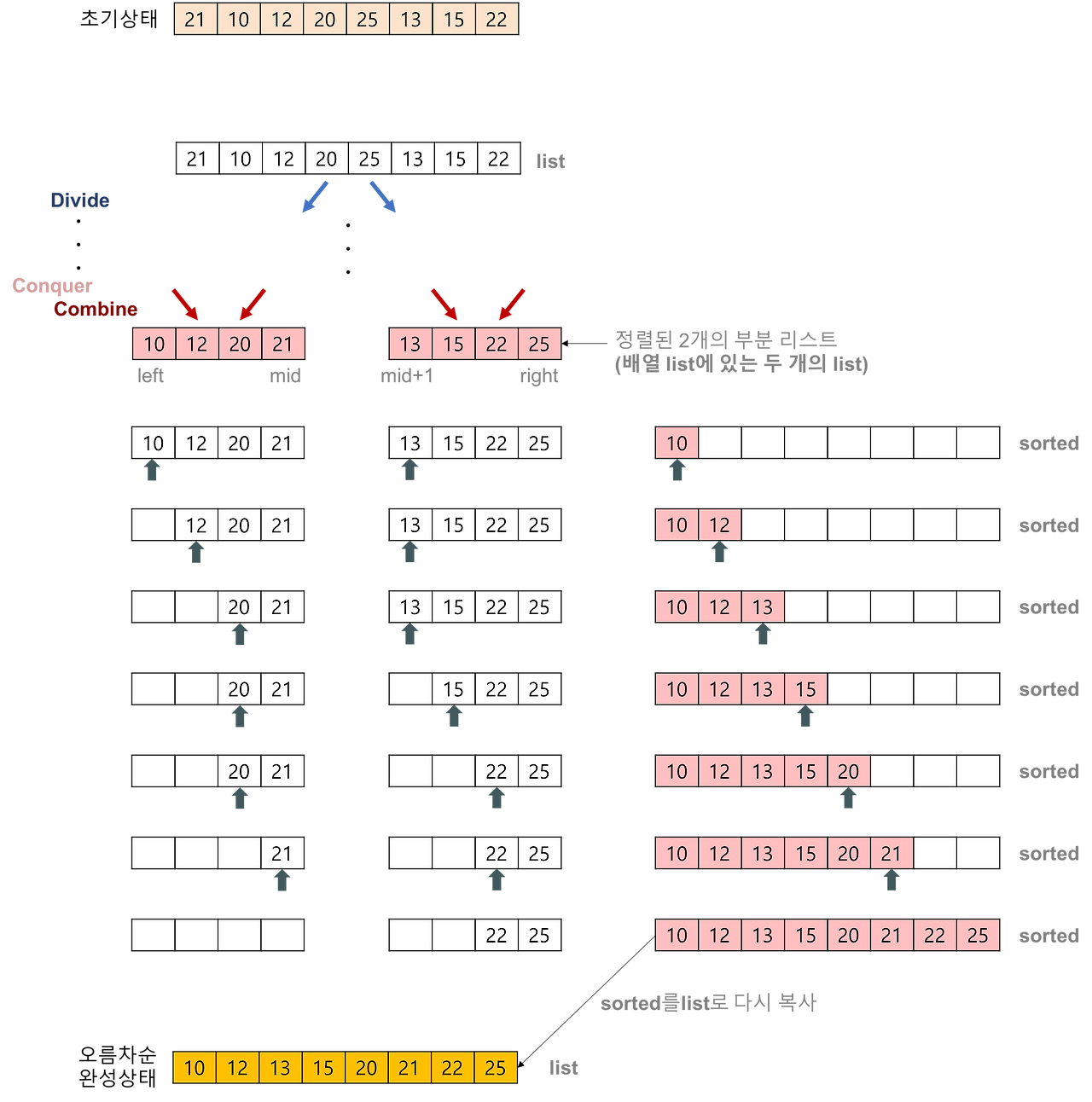
병합 정렬 개념 : 분할 정복의 알고리즘중 하나의 정렬방식
배열을 반 으로 나눈뒤 크기가 1 이 될떄까지 계속 나눔
배열의 크기가 1이되면 정렬이됨
정렬된 두 배열을 하나로 합치면 배열 완성
ex ) [5, 3, 8, 6, 7]
중간 인덱스를 계산한다
중간 인덱스 = (시작인덱스 + 끝인덱스) / 2
result = ( 0 + 4 ) / 2 = 2 중간인덱스의 결과값은 2
2번 인덱스 즉 8이 중간값이 된다
1. 왼쪽
[ 5, 3, 8 ] -> [5, 3] + [8]
[5, 3] -> [5] + [3] -> [3, 5]
[3, 5] + [8] -> [3, 5, 8]
2.오른쪽
[6, 7] -> 정렬됨
3. 결과값 = [3, 5, 8] , [6, 7] 이 존재
첫번째 원소 3, 6 비교 3이 더 작음
첫번째 배열에 3 추가 [ 3 ]
두번째 원소 5와 6 비교 5가 더 작음
두번째 배열에 5 추가 [ 3, 5 ]
세번째 원소 8과 6 비교 6가 더 작음
세번째 배열에 6 추가 [ 3, 5, 6 ]
세번쨰 원소 8과 7 비교 7이 더 작음
네번째 배열에 6 추가 [ 3, 5, 6, 7]
남은원소 처리 8 추가
[3, 5, 6, 7, 8]
-------------- 만약 인덱스가 홀수 갯수 일경우 ------
개념 : 작게 나눈뒤 다시 합치면서 정렬
ex ) {5, 3, 8, 6}
1. 분할하기
ex ) [5, 3, 8, 6]
-> [5, 3], [8, 6]
2. 정복하기
[5,3] -> [3,5}
[8,6] -> [6,8]
3. 병합하기
[3, 5] + [6 + 8]
[ 3, 5, 6, 8]
시간복잡도 : 항상 O(N LOG N)
장점 : 안정적, 빠름
단점 : 추가 메모리가 필요하다
시간복잡도 : 모든경우 전부 O( N LOG N )
이유 : 배열을 계속 반으로 나누고 나누는 정렬 방식이라서
장점 : 최선 최악 평균 모드 O (NLOGN]이라 안정적이고 큰 데이터인경우 적합하다
안정정렬이다
단점 : 추가 메모리가 필요하다, 작은 배열에는 비효율적이다
병합 정렬 예시
#include <iostream>
#include <vector>
using namespace std;
void mergeSort(vector<int>& arr, int left, int right) {
if (left >= right) return;
int mid = (left + right) / 2;
mergeSort(arr, left, mid); // 왼쪽 정렬
mergeSort(arr, mid + 1, right); // 오른쪽 정렬
// 병합
vector<int> temp;
int i = left, j = mid + 1;
while (i <= mid && j <= right) {
if (arr[i] < arr[j])
{
temp.push_back(arr[i++]);
}
else
{
temp.push_back(arr[j++]);
}
}
while (i <= mid)
{
temp.push_back(arr[i++]);
}
while (j <= right)
{
temp.push_back(arr[j++]);
}
for (int k = 0; k < temp.size(); ++k)
{
arr[left + k] = temp[k];
}
}
void solution(vector<int>& arr) {
mergeSort(arr, 0, arr.size() - 1);
}
int main()
{
vector<int> arr = { 5, 3, 2, 8, 7, 10, 11 };
solution(arr);
for (int x : arr)
{
cout << x << " ";
}
return 0;
}
'C++ 프로그래머스 > Sort' 카테고리의 다른 글
| 프로그래머스(C++) - H-Index (1) | 2025.08.19 |
|---|---|
| 프로그래머스(C++) - 가장 큰 수 (0) | 2025.08.18 |
| 프로그래머스(C++) - k번째 수 (0) | 2025.08.18 |
| 프로그래머스(C++) - 명예의 전당(1) (0) | 2025.07.27 |
